1. 图解

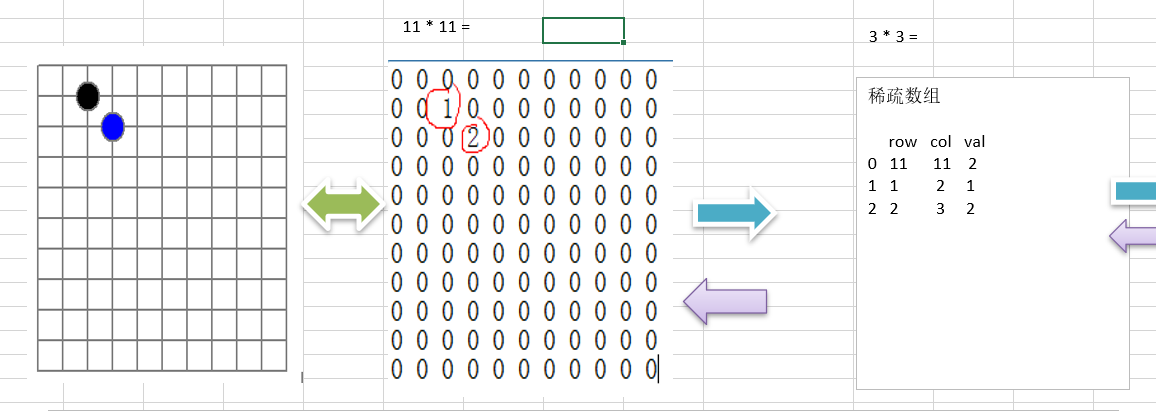
这个教程的讲解是以五子棋棋盘落子的应用场景来介绍的，棋盘就相当于一个二维数组，其中 0表示无子，1表示黑子，2表示蓝子。

2. 思路

2.1 二维数组转换成稀疏数组：

  1. 遍历原始的二维数组，获取有效数据的个数 sum；
  2. 根据有效数据个数 sum 创建一个稀疏数组 sparseArr int[sum + 1] [3];
  3. 将二维数组的有效数据存入到稀疏数组中；

2.2 稀疏数组转换成二维数组

  1. 先读取稀疏矩阵的第一行数据，根据第一行数据创建原始的二维数组，比如上图所示 beginArr int[11] [11];
  2. 再读取稀疏数组后面的几行数据，并赋值给原始的二维数组即可；

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
package com.self.sparsearray;

public class SparseArray {

    public static void main(String[] args) {

        //创建原始的二维数组
        //0:表示没有棋子 1：表示黑子 2：表示蓝子
        int chessArr1[][] = new int[11][11];
        chessArr1[1][2] = 1;//第二行第三列的是黑子
        chessArr1[2][3] = 2;//第三行第四列表示蓝子
        //输出原始的二维数组
        System.out.println("原始的二维数组:");
        for (int[] row : chessArr1) {
            for (int data: row){
                System.out.printf("%d\t",data);
            }
            System.out.println();
        }
        //将二维数组 转 稀疏数组思路
        //1.遍历原始的二维数组得到有效数据的个数
        int sum = 0;
        for (int i = 0; i < 11; i++) {
            for (int j = 0; j < 11;j++){
                if(chessArr1[i][j] != 0){
                    sum ++;
                }
            }
        }
        System.out.println("sum=" + sum);

        //2.创建对应的稀疏数组
        int sparseArr[][] =  new int[sum + 1][3];
        //3.给稀疏数组赋值
        //第一行
        sparseArr[0][0] = 11;
        sparseArr[0][1] = 11;
        sparseArr[0][2] = sum;

        //把二维数组有效数据遍历赋值给稀疏数组sparseArr中
        int count = 0; //count 用于记录是第几个非0数据
        for (int i = 0; i < 11; i++) {
            for (int j = 0; j < 11;j++){
                if(chessArr1[i][j] != 0){
                    count++;
                    sparseArr[count][0] = i;
                    sparseArr[count][1] = j;
                    sparseArr[count][2] = chessArr1[i][j];

                }
            }
        }
        //输出稀疏数组形式
        System.out.println();
        System.out.println("转换后得到的稀疏数组：");
        for (int i = 0; i < sparseArr.length; i++) {
            System.out.printf("%d\t%d\t%d\t\n", sparseArr[i][0],sparseArr[i][1],sparseArr[i][2]);
        }

        //==========================================================================
        //将稀疏数组恢复成原始的二维数组
        //1.先读取稀疏数组第一行，根据第一行数据，创建原始的二维数组
        int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];

        //2.读取稀疏数组的后几行(第二行开始)，并赋给原始的二维数组即可
        for (int i = 1;i< sparseArr.length ; i++){
            chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
        }

        //输出恢复后的二维数组
        System.out.println();
        System.out.println("恢复后的二维数组:");
        for (int[] row : chessArr2) {
            for (int data: row){
                System.out.printf("%d\t",data);
            }
            System.out.println();
        }
        
    }
}

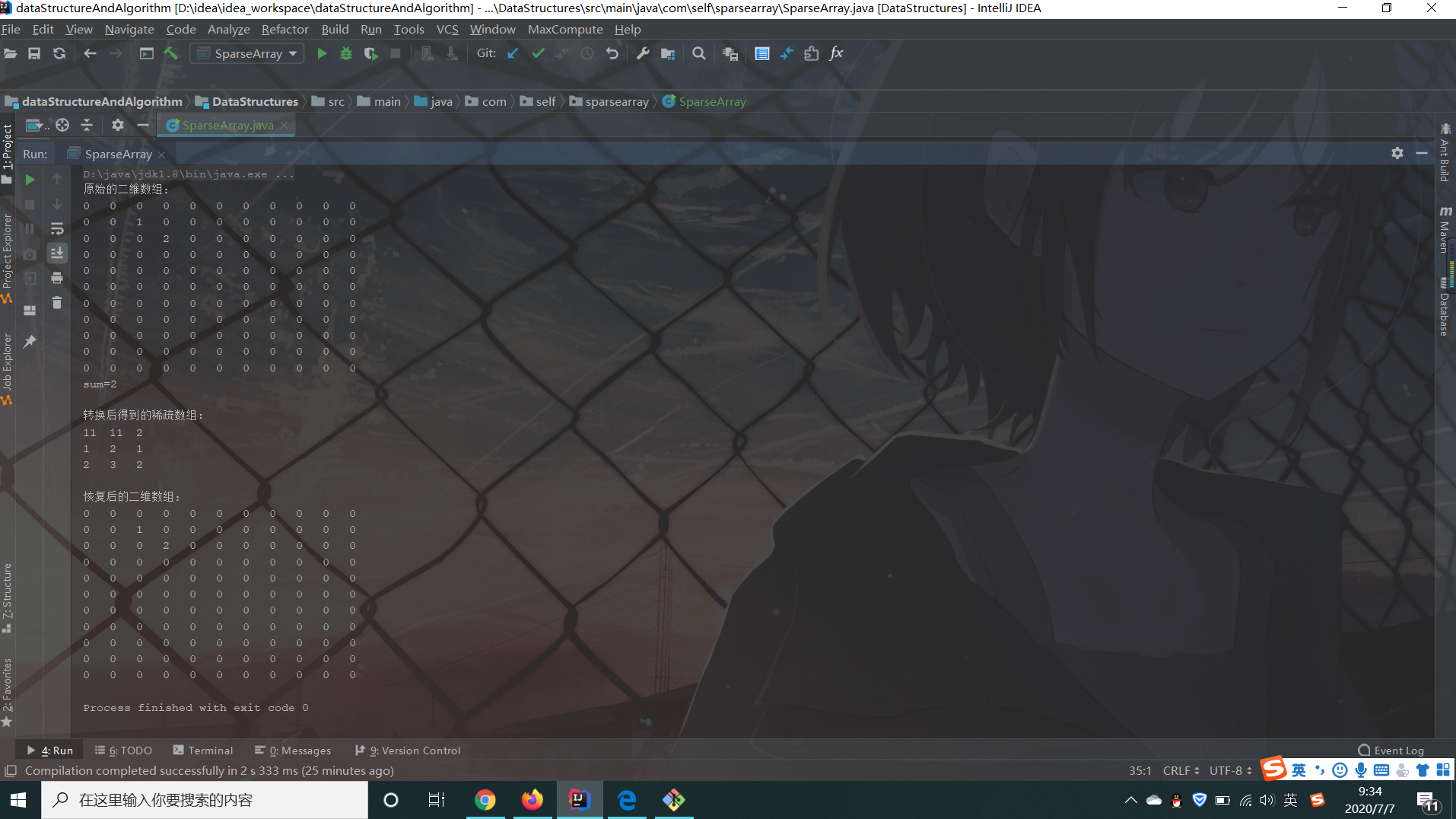
效果图：